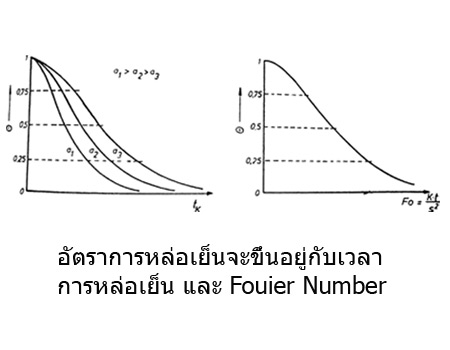
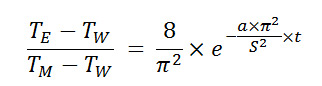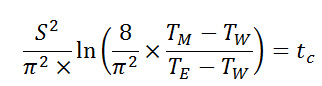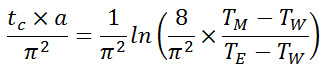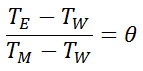เวลาในการหล่อเย็น

เวลาในการหล่อเย็น ( Cooling Time)

การหล่อเย็นเริ่มต้นเมื่อฉีดพลาสติกเต็มแม่พิมพ์ ซึ่งเกิดขึ้นในช่วงเวลา t_i ความร้อนส่วนใหญ่จะถ่ายเทออกไปในช่วงเวลาหล่อเย็น t_c คือเวลาหลังจากการฉีด จนถึงการปิดแม่พิมพ์และปลดชิ้นงาน การออกแบบระบบหล่อเย็น จะขึ้นอยู่กับส่วนของชิ้นงานที่ต้องหล่อเย็นเป็นเวลานานที่สุด ให้เย็นลงจนถึงอุณหภูมิปลดชิ้นงาน T_E

การแลกเปลี่ยนความร้อนระหว่างพลาสติกและสารหล่อเย็น เกิดขึ้นโดยการนำความร้อนในแม่พิมพ์  การนำความร้อนสามารถอธิบายได้ด้วย Fourier’s differential equation โดยใช้การคำนวณแบบ 1มิติก็พอ เพราะชิ้นงานฉีดพลาสติกมักจะใช้การแก้ปัญหาใน2มิติและถ่ายเทความร้อนออกในหนึ่งทิศทาง

ในกรณีของการถ่ายเทความร้อนแบบหนึ่งมิติ Fourier’s differential equation สามารถลดรูปได้เป็น

สัญลักษณ์ในสมการต่างๆเป็นดังนี้

a = การแพร่กระจายของความร้อน (ตร.ม/วินาที)

(ตร.ม/วินาที)

t = เวลา(วินาที)

t_c = เวลาในการหล่อเย็น(วินาที)

S = ความหนาของผนัง (ม.หรือ1000 มม.)

x = ระยะทาง (ม. หรือ 1000มม.)

= ความหนาแน่นของพลาสติก (กก/ลบ.ซม.)

k = การนำความร้อน (วัตต์/ม.k)

C_p =ความจุความร้อนจำเพาะ (จูล/กก.k)

T_E = อุณหภูมิปลดชิ้นงาน (^oC)

T_Emax = อุณหภูมิปลดชิ้นงานสูงสุด (^oC)

T_Emean = อุณหภูมิปลดชิ้นงานเฉลี่ย (^oC)

T_M = อุณหภูมิน้ำพลาสติก (^oC)

T_W = อุณหภูมิผนังคาวิตี้ (^oC)

อัตราการหล่อเย็น

F_O = Fourier number

สมมติว่าทันทีที่พลาสติกฉีดเสร็จ อุณหภูมิน้ำพลาสติกในคาวิตี้จะคงที่ทุกแห่ง คือ f(x),อุณหภูมิที่ผนังคาวิตี้สูงถึงค่าคงที่ T_w = f (t_c) และไม่เปลี่ยนแปลงดังนี้

เป็นคำตอบหนึ่งของ differential equation ถ้าพิจารณาเฉพาะจำนวนแรกของอนุกรม คือ

จะได้

หรือหาคำตอบในรูปของเวลาการหล่อเย็น

จัดรูปสมการใหม่เป็น

จะได้ตัวแปรไร้มิติของการหล่อเย็น (ตามภาพด้านบน)

ซี่งเรียกว่าอัตราส่วนอุณหภูมิเกิน และใช้แทนอัตราการหล่อเย็นได้

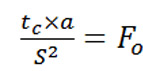คือ Fourier number ซึ่งไม่มีหน่วย

ถ้า = ค่าคงที่ อัตราส่วนการหล่อเย็นจะเท่าเดิม อัตราส่วนการหล่อเย็นที่ต่างกันสามารถแสดงโดยกราฟที่มี่หน่วย ตามภาพด้านบน

ถึงแม้การฉีดพลาสติกไม่เป็นไปตามเงื่อนไขที่ต้องการได้อย่างแน่นอน แต่จากประสบการณ์ก็สามารถคำนวณเวลาจากการหล่อเย็นได้แม่นยำเพียงพอ ในการฉีดเทอร์โมพลาสติกจะปลดชิ้นงานที่อัตราส่วนอุณหภูมิเท่าเดิมเสมอ นั่นคือ ด้วยอัตราการหล่อเย็นเท่าเดิม  ดังนั้น จึงหาค่าเฉลี่ยของการแพร่กระจายความร้อน (a) และการแพร่กระจายความร้อนประสิทธิผล (a_eff) ได้ สมการที่ใช้แทนการแพร่กระจายความร้อนจะไม่แน่นอน โดยเฉพาะกับโครงสร้างพลาสติกเป็นระเบียบ

Social tagging: การหล่อเย็นแม่พิมพ์ > เทอร์โมพลาสติก